Lubomir Kavalek
Huffington Post, September 21, 2010Chess Puzzles: Richard Reti's Marvelous Squares
A chessboard is a square, divided into 64 black and white squares. But there are more squares in chess, mostly invisible, as part of an amazing chess geometry hidden in chess players' minds.
One classic square is often used in pawn endgames when a king is chasing the enemy's passed pawn. The king doesn't have to walk in horizontal or vertical lines, he can run diagonally or zig-zag across the field. But he needs to be close enough to catch the pawn. How close?
The king has to walk into a square whose one side is defined as the distance between the pawn and its promoting square at the edge of the board.
We can use a famous study by Richard Reti as an example. The world-class player, creative chess composer and prolific writer published his amazing work in Ostrauer Morgenzeitung on December 4, 1921.
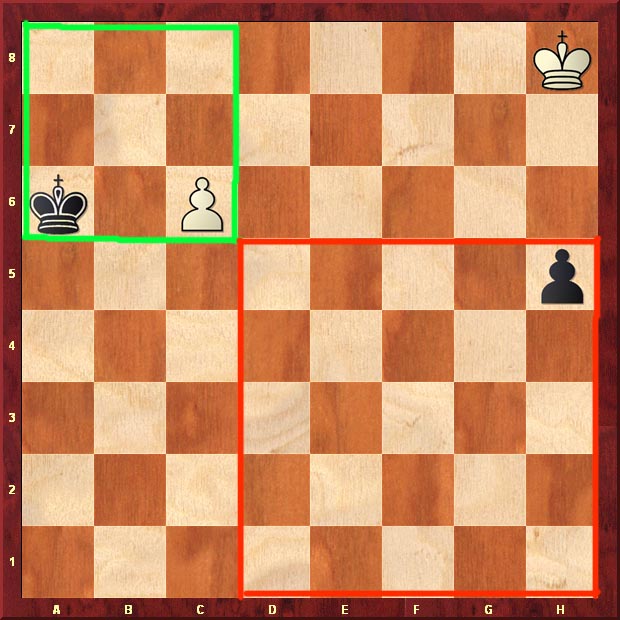
While the black king is in the (green) square and can snap up the white c-pawn anytime, the white king is out of the (red) square, unable to catch the black h-pawn. Reti makes the study work, blending both green and red squares into a beautiful solution. Can you find how white draws?
Other composers tried to expand on Reti's maneuver. Ladislav Prokes juggles the squares differently. The black pawn is far out of reach, but the white king, momentarily pinned to the edge of the board, finds a miraculous way to stop it.

Henri Rinck composed his version in 1922 and published it in the Revue Suisse d'Echecs in Basel. He also worked with squares, but added a line-geometry, the skewer, into the solution.

Solutions to all three studies appear next week.
No comments:
Post a Comment